KMU
396
MATERIALS
SCIENCE
Midterm
Examination
Solutions
Question 1. (18 pts)
a) (14 pts.)
§ For brass, the bonding is metallic
since it is a metal alloy.
§ For rubber, the bonding is covalent
with some van der Waals. (Rubber is composed primarily
of carbon and hydrogen atoms.)
§ For BaS,
the bonding is predominantly ionic (but with some covalent character) on the basis
of the relative positions of Ba and S in the periodic
table.
§ For solid xenon, the bonding is van
der Waals since xenon is an inert gas.
§ For bronze, the bonding is metallic
since it is a metal alloy (composed of copper and tin).
§ For nylon, the bonding is covalent
with perhaps some van der Waals. (Nylon is composed
primarily of carbon and hydrogen.)
§ For AlP
the bonding is predominantly covalent (but with some ionic character) on the basis
of the relative positions of Al and P in the periodic table.
b) (4 pts) Since the hydrogen bond is stronger than van der
Waals, HF will have a higher
melting temperature ) (19.4 vs. -85ºC)
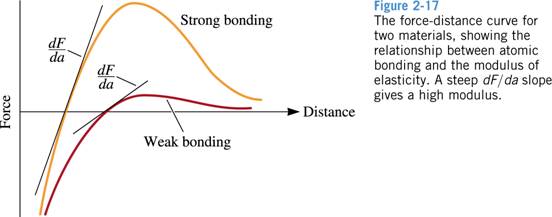
Question 2. (10 pts.)
Beryllium
and magnesium, both in the 2A column of the periodic table, are lightweight
metals. Which would you expect to have the higher modulus of
elasticity?
Explain,
considering binding energy and atom radii and using appropriate sketches
of force versus interatomic spacing.
Solution:
4 Be 1s22s2 E=42x106 psi rBe =1.143 Å
12 Mg 1s22s22p63s2
E =6x106 psi rMg =1.604 Å
Be
has higher melting and boiling T than Mg as shown on the periodic table on
pg.32 meaning Be has higher binding energy. In addition, Be
atoms are smaller than Mg atoms. Therefore smaller Be
electrons are held closer to the core therefore held more tightly, giving a
higher binding energy.
Be
Question 3. (12 pts.)
In this problem we are
asked to cite which of the elements listed form with Cu the three possible
solid solution types. For complete substitutional solubility the following criteria must be
met: 1) the difference in atomic radii
between Ni and the other element (ΔR%) must be less than ±15%, 2) the
crystal structures must be the same, 3) the electronegativities
must be similar, and 4) the valences should be the same, or nearly the
same. Below are tabulated, for the
various elements, these criteria.
Element ΔR% Structure negativity
Cu FCC 2+
C -44
H -64
O -53
Ag +13 FCC 0 1+
Al +12 FCC -0.4 3+
Co -2
Cr -2
Fe -3
Ni -3 FCC -0.1 2+
Pd +8 FCC +0.3 2+
Pt +9 FCC +0.3 2+
Zn +4
(a) Ni, Pd, and Pt meet
all of the criteria and thus form substitutional
solid solutions having complete solubility.
(b) Ag, Al, Co, Cr, Fe,
and Zn form substitutional solid solutions of
incomplete solubility. All these metals
have either
(c) C, H, and O form
interstitial solid solutions. These
elements have atomic radii that are significantly smaller than the atomic
radius of Cu.
Question
4. (20 pts.)
a) A material in which atomic bonding is predominantly ionic in nature is
less
likely to form a noncrystalline solid upon
solidification than a covalent material because covalent bonds are directional whereas ionic bonds are nondirectional; it is more difficult for the atoms
in a covalent material to assume positions giving rise to an ordered structure.
b) A crystal structure is described by both
the geometry of, and atomic arrangements within, the unit cell, whereas a
crystal system is described
only in terms of the unit cell geometry.
For example, face-centered cubic and body-centered cubic are crystal structures that belong to the
cubic crystal system.
c) The vacancy concentration in a crystal structure
increases with __temperature_.
d) The
surface energy of a single crystal depends on crystallographic orientation because the atomic packing is
different for the various crystallographic planes, and, therefore, the number
of unsatisfied bonds will vary from plane to plane.
e) The surface energy will be greater for an FCC (100) plane
than for a (111) plane because the (111) plane is more densely packed (i.e., has more nearest neighbor atoms in the plane); as a consequence,
more atomic bonds will be
satisfied for the (111) plane, giving rise to a lower surface energy.
Question 5. (20 pts.)
|
Peak No |
2θ (degrees) |
sin2θ |
sin2θ/0.1391 |
h2+k2+l2 |
(hkl) |
dhkl
(nm) |
|
1 |
43.8 |
0.1391 |
1 |
3 |
(111) |
0.2067 |
|
2 |
50.8 |
0.1840 |
1.3227 |
4 |
(200) |
0.1797 |
|
3 |
74.4 |
0.3655 |
2.6279 |
8 |
(220) |
0.1275 |
|
4 |
90.4 |
0.5035 |
3.6196 |
11 |
(311) |
0.1087 |
a) For each peak, in order to calculate the interplanar spacing we must employ Bragg’s law. For the first peak which occurs at 43.8o
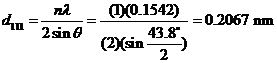
b) The first peak results by diffraction from (111) planes.
c) The h2+k2+l2 order of 3,4,8,11 is for an FCC crystal structure in which only those
peaks for which h, k, and l are all either odd or even will appear. Consequently, the
material could be Cu (Fe has
d) Computation of atomic radius R for FCC crystal structure is given by:
a=d111(1+1+1)1/2=0.2067(3)1/2=0.3580
nm
a=d200(4+0+0)1/2=0.1797(2)=0.3594
nm
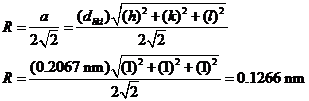
Similar computations are made for the other peaks which results are tabulated below:
Peak Index 2q dhkl(nm) R (nm)
200 50.8 0.1797 0.1271
220 74.4 0.1275 0.1275
311 90.4 0.1087 0.1274
Question
6 (20 pts.)
a)
b)
c)
The hardest material in the list would be the best choice for a
knife-blade. Therefore, cold rolled steel is the best choice.
d)
The toughest material, hot rolled steel, would be best for a construction
nail as nails should be able to resist high impact.