HOMEWORK 1

Q1. Write a general MATLAB® program to calculate the determinant of a 3-by-3 matrix using the spaghetti rule. Try your code for the following matrices. Check your answer using the det(A) command.

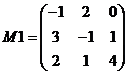
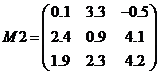
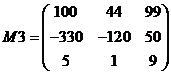
Hint: Write a script in an m-file. Remember

,

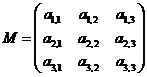i.e. M=[a_i,j] where i=1:3 and j=1:3.

When you define a 3-by-3 matrix in the command window, say M1, you should call the function you wrote in the m-file and the function will calculate the determinant.

For example the following commands when written in the command window should give detM1 calculated by your script and also the det(A) calculated by MATLAB®:

M1=[-1 2 0; 3 -1 1; 2 1 4];

detM1=MyDeterminant(M1) % MyDeterminant is the name of the function and your m-file

y=determinant-1 1; 2 1 4];

rminant.

e command window, say M1, you should call the function you wrote in the m-file and the func

Start your m-file as:

function [dM,dmM]=MyDeterminant(M)

[m,n]=size(M) % gives the size of the matrix for an m-by-n matrix (you may or may not need this line)

dM= ….. %This is where you calculate the determinant using the spaghetti rule

d1M=det(M) %Use the MATLAB® function det to calculate the determinant and check your result

dM %will write the value of dM on the command window

d1M %will write the value of d1M on the command window

Let me give you an example: The following is an m-file for a function named MySum.m that sums the elements of the matrix M

function [totalM]=SumFun(M) %the function returns totalM,

totalM=M(1,1)+M(1,2)+M(1,3)+M(2,1)+ M(2,2)+M(2,3)+M(3,1)+ M(3,2)+M(3,3) %Add the elements of the matrix

end

This code could alternatively be written as the following where M could be a matrix of any size:

function [totalM]=SumFun(M) % the function returns totalM,

[m,n]=size(M); % assigns the size of M matrix to m and n

i=1; %start at i=1

j=1; %start at j=1

totalM=0; %start at totalM=0

for i=1:m % nested loop: increment i by 1 until m

for j=1:n,

totalM=totalM+M(i,j);

end

end

totalM

To run this function, go to the command window and write a matrix

For example:

>> A=[ 1 2 3 4; 12 2 4 2; 34 3 1 6; 0 2 5 3]

>> SumFun(A) %will give you the following answer

totalM =

84

PS: Those who write the code for a size of any matrix will get bonus points!

Q2. Solve the following set of equations in MATLAB® using

1. Matrix inversion

2. Gauss-Jordan relation

3. Cramer’s rule

x₁ + x₂ + 3 x₃ = 1

x₁ + 2 x₂ + 5 x₃ = 2

3 x₁ + x₂ + x₃ = 1