KMU206 Numerical Analysis Instructor: Dr. Selis Önel HOMEWORK 1 Submit electronically at kmu206@gmail.com

Q1. Write a general MATLAB® script in an m-file to solve a linear system of three equations and three unknowns using Cramer’s rule.

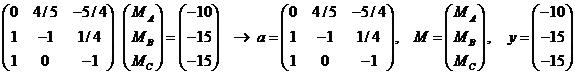
The script should first

- check if the coefficient matrix is square. If the [a] is not square it should display an error message on the command window and stop, otherwise continue,

- calculate the determinant of [a]. If det(a) is equal to zero, then it should display an error message and stop, otherwise continue

Once the results are obtained by the script

- use the left-division (Gauss-elimination) operation of MATLAB® (x=a\y) to get the results

- compare both results. If the results are close, write “Cramer’s rule results match with those of left-division in MATLAB®”.

Q2. Write a MATLAB® function in an m-file to solve a linear square system of any size using Cramer’s rule given the coefficient matrix [a] and the vector of inhomogeneous terms [y]. This function will do the same as the script in Question 1, but it will apply to a square matrix of any size.

Hints: Remember

,

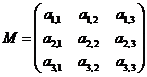i.e. M=[a_i,j] where i=1:3 and j=1:3.

To get the size of the matrix use:

[m,n]=size(M);

If m==n, then the matrix is square

Let me give you an example: The following are examples of m-files for a function named MySum.m that sums the elements of the matrix M

function [totalM]=SumFun(M) %the function uses the given matrix M and returns totalM,

totalM=M(1,1)+M(1,2)+M(1,3)+M(2,1)+ M(2,2)+M(2,3)+M(3,1)+ M(3,2)+M(3,3) %Add the elements of the matrix

end

This code could alternatively be written as the following where M could be a matrix of any size:

function [totalM]=SumFun(M) % the function returns totalM,

[m,n]=size(M); % assigns the size of M matrix to m and n

i=1; %start at i=1

j=1; %start at j=1

totalM=0; %start at totalM=0

for i=1:m % nested loop: increment i by 1 until m

for j=1:n,

totalM=totalM+M(i,j);

end

end

totalM

To run this function, go to the command window and write a matrix

For example:

>> A=[ 1 2 3 4; 12 2 4 2; 34 3 1 6; 0 2 5 3]

>> SumFun(A) %will give you the following answer

totalM =

84