KMU-206 MIDTERM II

Instructor: Selis Önel

May 2, 2008

You are allowed to take with you an A4 size information sheet handwritten by yourself.

Please make sure you have written your name on the question sheet, your information sheet and the answer sheets.

Question 1. (30 pts)

The constant pressure heat capacity of a gas can be written as a function of temperature in the form given by: Cp(T) = A + B*T + C*T² + D*T³ + …

The heat capacities for a certain gas measured at various temperatures are listed below and plotted on the figure:

Heat Capacity, Cp J/(gmol.K)	Temperature,T Kelvin
26.95	300
27.40	400
28.00	600

What would be the heat capacity of this gas at 500 K, 800 K and 1000 K ?

a) Write the appropriate Cp equation

b) Determine the constant parameters (A, B, …) of the Cp equation using one of the Gauss Elimination or Gauss Jordan methods

c) Find the Cp values at 500 K, 800 K and 1000 K and plot these points on the graph

Please show all steps of your work and calculations.

Question 2. (40 pts)

Find the positive real zero of f(x) using the bisection method:

f(x) = 2x³+(13/5)x²-4x-(12/5)

a) Plot a rough graph of the function to show the function has a positive real zero (Calculate the value of the function at least at four points)

b) Select an interval [a,b] that brackets the root to start the iterations

c) Show at least three consecutive iterations and for each iteration compare the absolute value of the difference between a and b with the tolerance (tol=0.01), i.e., check if |b-a|<0.01

Question 3. (15 pts)

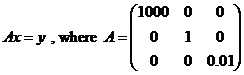
a) Find the determinant of A (|A|=?)

b) Find the eigen values of the above system of linear equations (λ₁, λ₂, … λ_n =?)

c) Find the condition of A (cond(A)=?)

Is the system Ax=y a stable system (Is this system ill-conditioned or not), why?

Question 4. (15 pts)

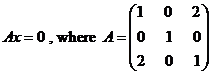
a) Write the characteristic equation (polynomial) for the coefficient matrix A

b) Find the roots of the characteristic equation and determine the eigen values

c) Determine the eigen vectors