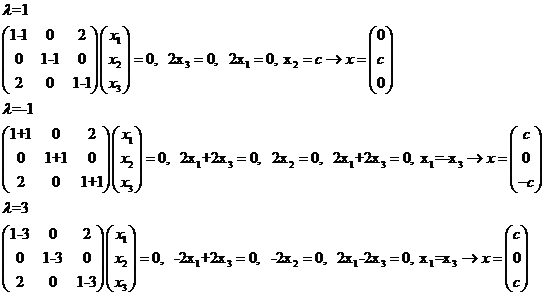KMU-206 MIDTERM II Solutions
Instructor: Selis Önel
Question 1.
(30 pts)
a)
In order to be able to fit a unique polynomial to the three data points
given, the equation should have three unknown coefficient that we can determine
uniquely. Therefore:
Cp(T) = A + B*T + C*T2
b)
Writing the equation at three data points gives:
26.95 = A +
B*(300) + C*(300)2
27.40 = A +
B*(400) + C*(400)2
28.00 = A +
B*(600) + C*(600)2
This linear
system of equations can be solved for A, B and C uniquely by using either of
the Gauss elimination or Gauss-Jordan methods.
Writing the
above equations in matrix form gives:
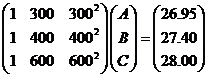
Using the Gauss
elimination method:
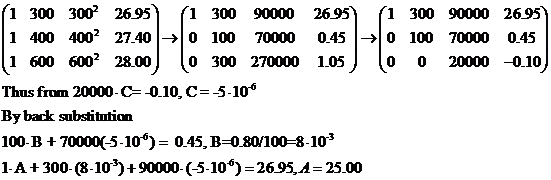
Using the Gauss-Jordan
method
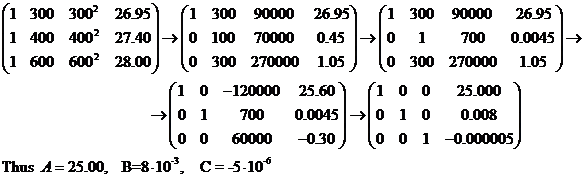
c)
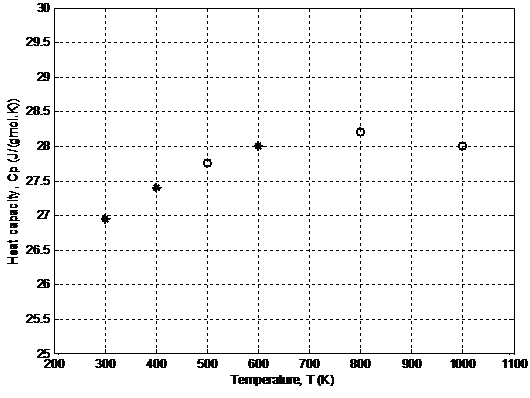
Cp(500) = 25 + 0.008(500) + (-0.000005)(500)2
= 27.75 J/(gmol.K)
Cp(800) = 28.20 J/(gmol.K)
Cp(1000) = 28.00 J/(gmol.K)
Question 2. (40 pts)
Find the positive real
zero of f(x) using the bisection method:
f(x) = 2x3+(13/5)x2-4x-(12/5)
a) f(0)=
-2.4000, f(0.5)= -3.5000, f(1)= -1.8000, f(1.5)= 4.2000
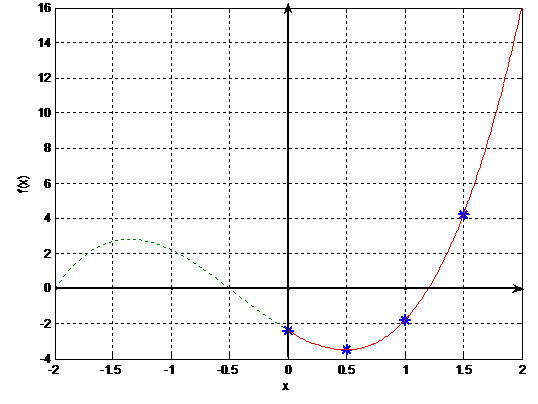
b)The graph and the function values calculated above show that there should
be a positive root for x values between 1 and 1.5. Therefore, it is possible to
select [a,b]=[1,1.5]
c) The iterations using bisection method in the
interval [1,1.5] are:
Step a
b
m f(a) f(b) f(m) |b-a|
1.0000 1.0000 1.5000
1.2500 -1.8000 4.2000
0.5688 0.5000 > 0.01
2.0000
1.0000 1.2500 1.1250
-1.8000 0.5688 -0.7617
0.2500 > 0.01
3.0000
1.1250 1.2500 1.1875
-0.7617 0.5688 -0.1345
0.1250 > 0.01
4.0000
1.1875 1.2500 1.2188
-0.1345 0.5688 0.2075
0.0625
5.0000
1.1875 1.2188 1.2031
-0.1345 0.2075 0.0341
0.0313
6.0000
1.1875 1.2031 1.1953
-0.1345 0.0341 -0.0508
0.0156
7.0000
1.1953 1.2031 1.1992
-0.0508 0.0341 -0.0085
0.0078
bisection has converged as
0.0078<0.01, and x ~ 1.1992
Question 3. (15 pts)
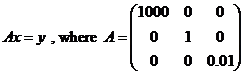
a)
A is a square diagonal matrix, therefore
|A|=(1000)(1)(0.01)=10
b)
A is a square diagonal matrix, therefore its eigen
values can be found immediately using the diagonal elements: λ1=1000,
λ2=1, λ3 =0.01
c)
For a square symmetric matrix, the condition number can be determined as
the ratio of the largest eigen
value to the smallest. cond(A)= λmax/
λmin=1000/0.01=100000
As the condition number
for this system is too large, the system is ill-conditioned and not stable.
Question 4. (15 pts)
a)
The characteristic equation (polynomial) for the coefficient matrix A can
be obtained by setting det[A-λI]
= 0
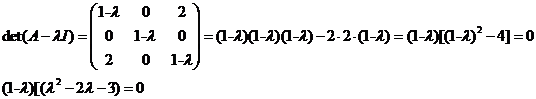
b)
The characteristic equation found above can be simplified as
(1-λ)(λ+1)(λ-3) = 0 , where the λ values can be determined
as: λ1=1, λ2=-1, λ3 = 3
c)
The eigen vectors can be found as: